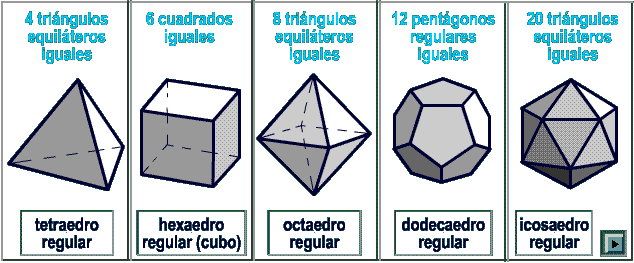
VOLUMEN DE CILINDROS
1.- Observad lo que sucede en la escena al variar los valores del radio y de la altura.
2.- ¿Cuál es el volumen de un cilindro de 1 cm de radio y 1 cm de altura o generatriz?. Varía el valor de laaltura desde 1 hasta 3 cm, de 0,5 en 0,5 cm.
3.- Halla los volúmenes de cilindros cuya alturas es de 1 cm y con radios: 1; 1,25; 1,5 y 2 cm, respectivamente.
4.- Repite las actividades 2 y 3 para una altura de 2 cm.
5.- Intenta hallar una expresión que permita calcular el volumen de un cilindro, conocidos su radio y su altura.
6.- Comprueba la validez de la expresión hallada en la actividad anterior calculando los volúmenes de los cilindros de la actividad 3.
7.- Calcula la altura de un depósito cilíndrico de 3 m de radio y 282,6 m3 de volumen. Si ese volumen fuera el volumen interior, ¿cuántos litros de agua se podrían almacenar en dicho depósito?
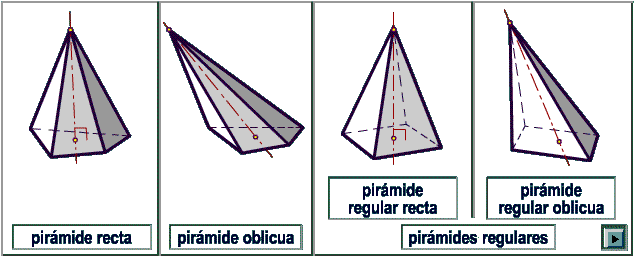
VOLUMEN DE PIRÁMIDES
1.- Mueve la barra de desplazamiento hasta su tope derecho. ¿Qué observas?
2.- Hasta dónde se llena el vaso en forma de prisma?.
3.- Pulsa el botón Inicio. Modifica los valores de la altura y de la arista de la base. Luego ve moviendo la barra de desplazamiento hasta llegar a su tope derecho. Repite estas operaciones para diferentes valores de la altura y de la arista de la base. Anota el resultado de tus observaciones.
4.- A la vista de lo observado en las actividades anteriores, ¿cuál es la relación entre el volumen de la pirámide y del prisma?. Recuerda que ambos tienen la misma altura y lamisma arista básica, además del mismo número de caras.
5.- Ahora ya debes poder escribir una expresión que permita calcular el volumen de una pirámide. Parte del resultado de la actividad anterior y de la expresión del volumen de un prisma.
VOLUMEN DE CONOS
1.- Mueve el cursor de la barra de desplazamiento hasta su tope derecho. ¿Qué sucede?
2.- ¿Qué parte del vaso se ha llenado?
3.- Después de pulsar el botón Inicio, modifica los valores de la altura y del radio. Vuelve a desplazar el cursor de la barra de desplazamiento hasta su tope derecho. Repite estas operaciones con nuevos valores de los parámetros de la escena. Anota el resultado de tus observaciones.
4.- ¿Qué relación existe entre el volumen de un cono y el volumen de un cilindro, dealturas y radios de las bases iguales?
5.- Para variar, ¿cómo podríamos calcular el volumen de un cono conociendo su altura y el radio de su base?. Recuerda lo hecho en el apartado anterior.
VOLUMEN DE ESFERA
1.- Varia los valores del Radio y observa el cambio correspondiente en el volumen.
2.- ¿Cuál es el volumen de una esfera de 2,4 cm de radio?
3.- Una esfera tiene un volumen de 15,6 cm3, ¿cuánto mide su radio?.
4.- Una copa de helado contiene tres bolas idénticas. Si entre las tres suman un volumen de 196,35 cm3, ¿cuál es su diámetro?.
5.- ¿Cuántos decilitros (dl) de helado contenía la copa de la actividad anterior?.
CUERPOS IRREGULARES
1.- Variad el valor del parámetro Figura. Observad los cuerpos que aparecen y los datos que acompañan a cada uno.
2.- Para cada cuerpo calculad su volumen. Explicad el proceso que empleéis en vuestro cuaderno de trabajo.
3.- Calcula el volumen del cuerpo que se obtiene al sustituir la pirámide y el prisma de la figura 3, por sendassemiesferas de radio el radio del cilindro central.
4.- Si de la cuarta figura de la escena te dijeran que los tres cuerpos que la componen tienen la misma altura, y el largo del paralelepípedo inferior fuera el doble de la arista del prisma triangular y su anchura fuera lacuarta parte de su altura, la pirámide tuviera igual altura que su arista y la altura total del cuerpo fuera de1,2 metros, ¿cuál sería su volumen?
Para poder hacer más ejercicios podéis visitar las siguientes páginas
http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena10/2esoquincena10.pdf
http://www.vitutor.com/geo/esp/v_e.html
http://www.vitutor.net/2/2/8.html
http://www.vitutor.com/geo/esp/vActividades.html
https://sites.google.com/site/profematesibq/09-06-11-ejercicios-areas-y-volumenes-cuerpos-geometricos
http://mimosa.pntic.mec.es/clobo/geoweb/revol1.htm